本文参考自 R 语言求圆周率：基于蒙特卡洛方法和《统计建模与 R 软件》。

蒙特卡洛方法介绍

蒙特卡洛（Monte Carlo）方法，又称为蒙特卡洛模拟，或统计试验方法或随机模拟等。所谓模拟就是把某一现实的或抽象的系统的部分状态或特征，用另一个系统（称为模型）来代替或模仿，在模型上作实验称为模拟实验，所构造的模型为模拟模型。

蒙特卡洛方法的基本思想是将各种随机事件的概率特征（概率分布、数学期望）与随机事件的模拟联系起来，用试验的方法确定事件的相应概率与数学期望。因而，蒙特卡洛方法的突出特点是概率模型的解是由试验得到的，而不是计算出来的。此外，模拟任何一个实际过程，蒙特卡洛方法都需要用到大量的随机数，计算量很大，人工计算是不可能的，只能在计算机上实现。

计算机技术的发展，使得蒙特卡罗模拟得到快速的普及。现代的蒙特卡罗模拟，已经不必亲自动手做实验，而是借助计算机的高速运转能力，使得原本费时费力的实验过程，变成了快速和轻而易举的事情。它不但用于解决许多复杂的科学方面的问题，也被项目管理人员经常使用。

蒙特卡洛方法在求圆周率方面具有独特的特点，以下是它在实际应用中的优缺点：

优点：蒙特卡洛方法基于概率统计的思想，通过模拟随机事件（如在正方形区域内随机撒豆子）来逼近结果。其原理简单易懂，不需要复杂的数学推导和高深的算法知识，对于初学者来说是一种很好的理解圆周率计算以及概率与几何关系的方式。在实际编程实现时，代码结构相对简单，通过基本的随机数生成和计数操作就能完成模拟过程。该方法不受问题的维度和复杂性限制，无论是二维平面上求圆周率，还是在更高维度的复杂几何形状或积分计算中，都可以通过适当的方式进行随机抽样模拟。由于蒙特卡洛模拟是通过多次独立的随机试验来进行的，各个试验之间相互独立，因此非常适合并行计算，尤其适用于大规模模拟计算的场景。

缺点：收敛速度慢。蒙特卡洛方法的结果收敛到真实值的速度相对较慢。从理论上来说，其误差与抽样次数 $n$ 的平方根成反比，这意味着如果想要获得较高精度的结果，就需要进行大量的随机试验。例如，要将圆周率的估计误差缩小到原来的十分之一，抽样次数需要增加到原来的一百倍，计算量会大幅增长，在对计算时间有严格要求的场景下，这可能是无法接受的。

蒙特卡洛方法估算圆周率核心原理

我们先画一个示例图，如下图所示。图中包含一个半径为 1 的单位圆，外接一个正方形。

# 图形参数设置
opar = par(no.readonly = TRUE)
on.exit(par(opar), add = TRUE)
par(pty = "s")  # 保持 1:1 比例

# 绘制单位圆
theta = seq(0, 2 * pi, length.out = 100)
plot(
  x = cos(theta), 
  y = sin(theta), 
  col = "red", 
  lwd = 2, 
  type = "l", 
  bty = "n",
  xlab = "", 
  ylab = "",
)

# 绘制外接正方形
rect(
  xleft = -1, 
  ybottom = -1, 
  xright = 1, 
  ytop = 1,
  border = "blue", 
  lwd = 2
)

# 生成并绘制随机点
set.seed(123)
get_points = \(n) {
  df = data.frame(
    x = runif(n, min = -1, max = 1), 
    y = runif(n, min = -1, max = 1)
  )
  return(df)
}

points_data = get_points(200)

points(
  points_data$x, 
  points_data$y, 
  pch = 19, 
  col = "green"
)

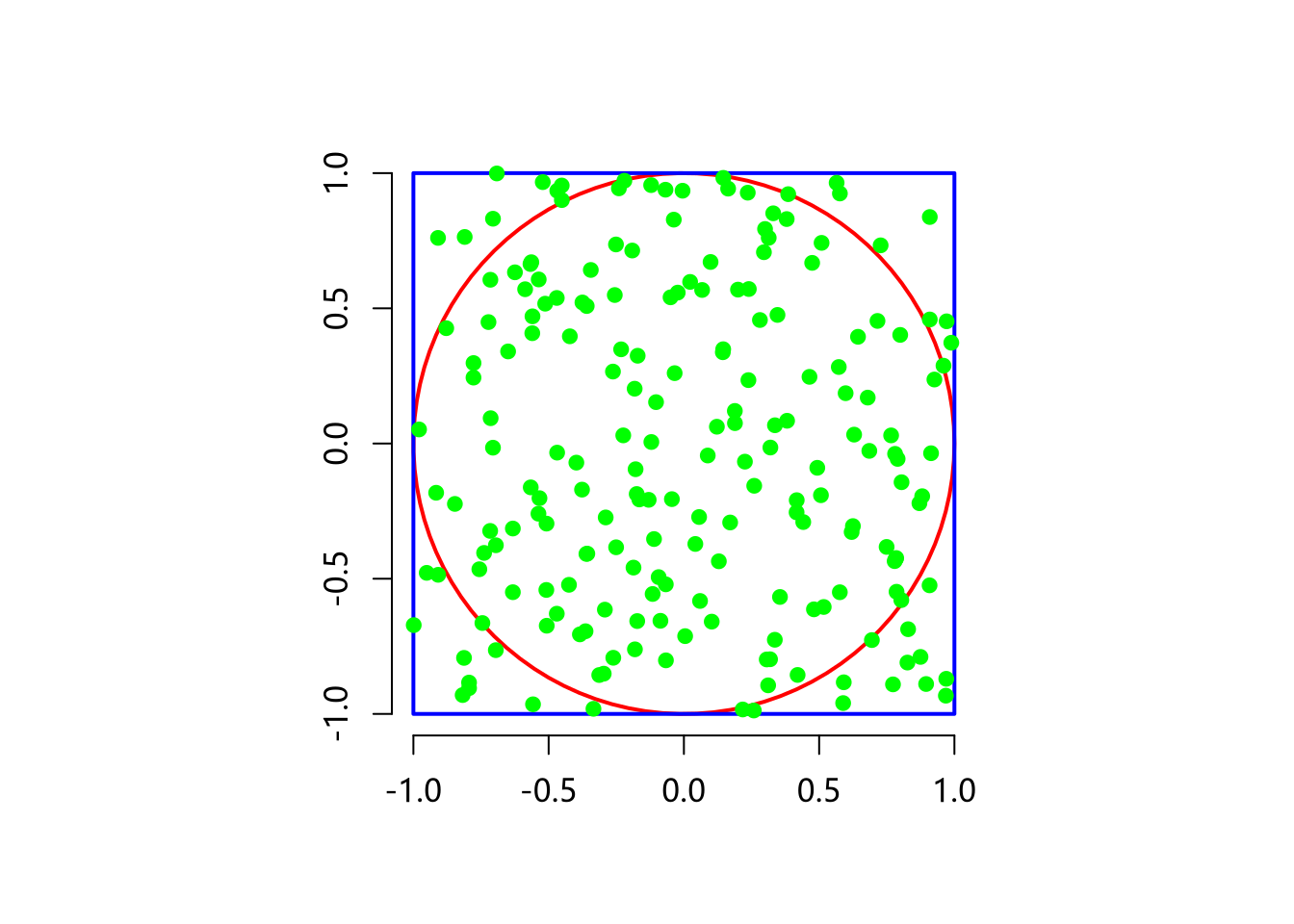
图上，圆的半径为 1，圆的面积就是 $\pi$，单位圆外接正方形的面积为 4。

理论上，如果我们往单位圆的外接正方形内随机撒豆子，假设豆子落在圆中的概率为 $p$，这个概率正好等于单位圆在外接正方形中的面积占比，公式表示如下：

$$ p = \frac{\pi}{4} $$

实践中，假设我们要向单位圆的外接正方形内随机撒 $n$ 个豆子，豆子落在圆内的数量为 $k$，那么豆子落在圆内的数量 $k$ 除以撒在正方形内豆子数量 $n$ 就得到了豆子落在圆中概率的估计 $\hat{p}$，公式表示如下：

$$ \hat{p} = \frac{k}{n} $$

每实验一次（撒一次豆子）就构成了一次豆子落在圆中概率的估计。估计值的期望值为 $p$，公式表示如下：

$$ E(\hat{p}) = p $$

根据上面的公式很容易推导出：

$$ \pi = p * 4 = E(\hat{p}) * 4 $$

此时估计 \(\pi\) 就转化为估计 $p$ 的问题:

$$ \hat{\pi} = \hat{p} * 4 = \frac{k}{n} * 4 $$

根据大数定理和中心极限定理，假设我们要撒 $n$ 个豆子，当 $n$ 趋于无穷大时，豆子落在圆中个数与豆子落在正方形内的个数之比 $\hat{p}$ 依概率收敛于真实 $p$（以 $p$ 为极限）。换句话说，$n$ 越大，估计的 $\pi$ 就会相对越准确。我们可以通过增加 $n$ 逐步逼近真实的 \(\pi\)。

代码实现

# 编写估计圆周率的函数
set.seed(123)
pi_hat = \(n) {
  df = get_points(n)
  mean(df$x^2 + df$y^2 < 1) * 4
}

# 做 9 次撒豆子实验
n = 10^(0:8)

# 生成估计的圆周率
result = lapply(n, pi_hat)
names(result) = n
print(result)

#> $`1`
#> [1] 4
#> 
#> $`10`
#> [1] 2.4
#> 
#> $`100`
#> [1] 3.48
#> 
#> $`1000`
#> [1] 3.18
#> 
#> $`10000`
#> [1] 3.156
#> 
#> $`1e+05`
#> [1] 3.14364
#> 
#> $`1e+06`
#> [1] 3.142608
#> 
#> $`1e+07`
#> [1] 3.141214
#> 
#> $`1e+08`
#> [1] 3.141456

从估计的结果来看，随着撒豆子数量的增加，圆周率估计值 $\hat{\pi}$ 总体上越来越接近真实的 $\pi = $ 3.1415927。为了更清楚地观察到撒豆子数量 $n$ 的变化对 $\hat{\pi}$ 的影响，有必要做一个收敛趋势图。

# 提取圆周率估计值
pi_hat_value = unlist(result)

# 绘制收敛曲线（撒豆子数量取对数，便于观察趋势）
plot(
  x = log10(n), 
  y = pi_hat_value,
  type = "b", 
  pch = 19, 
  col = "blue",
  xlab = "log10(撒豆数量)", 
  ylab = "π 估计值",
  main = "蒙特卡洛方法估计 π 的收敛趋势",
  ylim = c(2, 4)
)

# 添加真实 π 参考线
abline(h = pi, col = "red", lty = 2, lwd = 1.5)

# 添加数据点注释（关键点位）
key_points = c(2, 4, 6, 8)
for (i in key_points) {
  text(
    log10(n[i]), 
    pi_hat_value[i],
    paste(
      "n =", n[i], 
      "\nπ ≈", round(pi_hat_value[i], 6)
    ),
    pos = 1, 
    cex = 0.8
  )
}

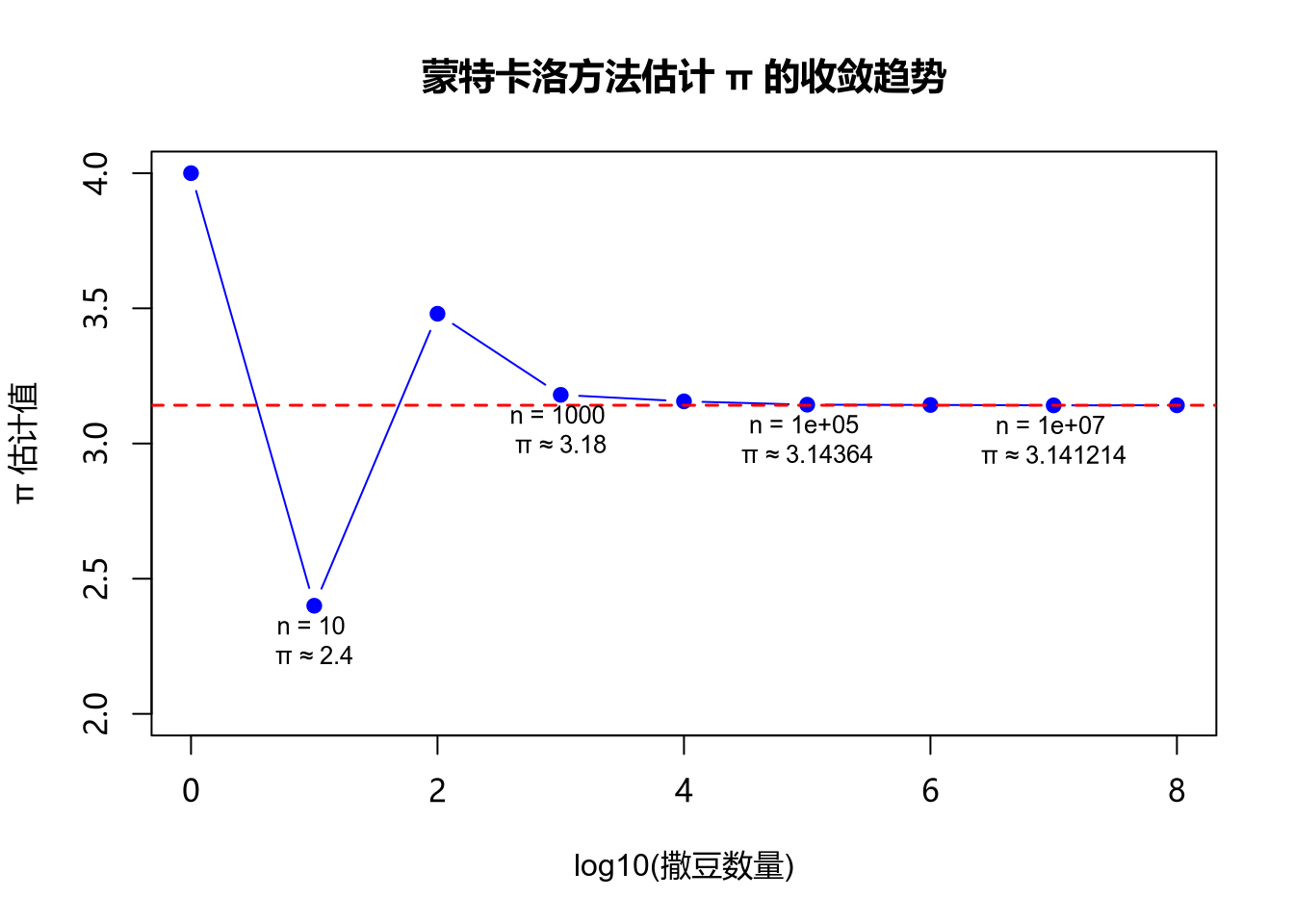
注：图上红色虚线表示真实的 $\pi$ 值 ，蓝色圆点表示 $\pi$ 的估计值 $\hat{\pi}$。

圆周率区间估计

上述估计是一个点估计，下面我们讨论蒙特卡洛方法估计圆周率区间估计

中心极限定理表明：设从均值为 $\mu$、方差为 $\sigma^2$ 的任意一个总体中抽取样本量为 $n$ 的样本，当 $n$ 充分大时，样本均值 $\overline{X}$ 的抽样分布近似服从均值为 $\mu$、方差为 $\frac{\sigma^2}{n}$ 的正态分布，即：

$$ \overline{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) $$

在蒙特卡洛估计概率的问题中，每次撒豆子是否落在圆内可以看作是独立同分布的伯努利试验。设随机变量 $X_i$ 表示第 $i$ 次撒豆子是否落在圆内，落在圆内 $X_i=1$，否则 $X_i=0$，其均值为 $E(X_i)=p$（真实的落在圆内的概率）,方差为 $Var(X_i)=p(1-p)$。

那么 $n$ 次撒豆子后，落在圆内的点的比例 $\hat{p}=\frac1n\sum_{i=1}^nX_i$ 。当 $n$ 足够大时，根据中心极限定理，$\hat{p}$ 近似服从正态分布：

$$ \hat{p}\sim N\left(p,\frac{p(1-p)}n\right) $$

将 $\hat{p}$ 标准化得到标准正态分布：

$$ Z = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \sim N(0,1) $$

在 95% 置信水平下，双侧分位数 $z_{\alpha/2}$ 满足：

$$ P(-z_{\alpha/2} < Z < z_{\alpha/2}) = 0.95 $$

其中 $P(Z < -z_{\alpha/2}) = P(Z > z_{\alpha/2}) = \frac{1-0.95}{2} = 0.025$，查标准正态分布表得 $z_{\alpha/2} = 1.96$。代入后可得：

$$ P\left(-1.96 < \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} < 1.96\right) = 0.95 $$

对不等式变形，得到 $\hat{p}$ 的置信区间：

$$ p - 1.96 \times \sqrt{\frac{p(1-p)}{n}} < \hat{p} < p + 1.96 \times \sqrt{\frac{p(1-p)}{n}} $$

由于 $\hat{\pi} = 4\hat{p}$，将 $\hat{p}$ 的置信区间两边乘以 4，得到 $\hat{\pi}$ 的 95% 置信区间：

$$ \pi - 1.96 \times \sqrt{\frac{p(1-p)}{n}} \times 4 < \hat{\pi} < \pi + 1.96 \times \sqrt{\frac{p(1-p)}{n}} \times 4 $$

注意：在实际应用中，由于 $\pi$ 和 $p$ 是未知的，我们通常使用 $\hat{\pi}$ 和 $\hat{p}$ 分别代替 $\pi$ 和 $p$ 来计算标准误差。因此，实际的区间估计公式为：

$$ \hat{\pi} - 1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n-1}} \times 4 < \hat{\pi} < \hat{\pi} + 1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n-1}} \times 4 $$