异方差:诊断与处理
楚新元 / 2021-09-06
对于模型,如果出现 \(Var(u_{i}) = σ_{i}^2\),即对于不同的样本点,随机误差项的方差不再是常数,而互不相同,则认为出现了异方差性(Heteroscedasticity)。古扎拉蒂《经济计量学精要》表 9-2 给出了 523 个工人的工资(每小时,美元)、教育(受教育年限)、经验(工龄) 等数据。本例只考虑工资与教育和经验的关系。
载入数据
options(digits = 4)
library(readxl)
library(dplyr)
library(kableExtra)
data = read_xls(
"data/Table9_2.xls",
skip = 5,
n_max = 523
)
data %>%
select(Wage, Educ, Exper) %>%
slice(1:20) %>% # 此处只展示前 20 个样本
kable() %>%
kable_styling(
bootstrap_options = "striped",
font_size = 14
)
| Wage | Educ | Exper |
|---|---|---|
| 5.10 | 8 | 21 |
| 4.95 | 9 | 42 |
| 6.67 | 12 | 1 |
| 4.00 | 12 | 4 |
| 7.50 | 12 | 17 |
| 13.07 | 13 | 9 |
| 4.45 | 10 | 27 |
| 19.47 | 12 | 9 |
| 13.28 | 16 | 11 |
| 8.75 | 12 | 9 |
| 11.35 | 12 | 17 |
| 11.50 | 12 | 19 |
| 6.50 | 8 | 27 |
| 6.25 | 9 | 30 |
| 19.98 | 9 | 29 |
| 7.30 | 12 | 37 |
| 8.00 | 7 | 44 |
| 22.20 | 12 | 26 |
| 3.65 | 11 | 16 |
| 20.55 | 12 | 33 |
建立回归模型
model = lm(Wage ~ Educ + Exper, data = data)
summary(model)
#>
#> Call:
#> lm(formula = Wage ~ Educ + Exper, data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -8.27 -2.85 -0.59 2.01 36.15
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -4.5245 1.2393 -3.65 0.00029 ***
#> Educ 0.9130 0.0822 11.11 < 2e-16 ***
#> Exper 0.0968 0.0177 5.46 7.2e-08 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.62 on 520 degrees of freedom
#> Multiple R-squared: 0.195, Adjusted R-squared: 0.192
#> F-statistic: 63 on 2 and 520 DF, p-value: <2e-16
$$ \widehat{Wage} = -4.5245 + 0.913 * Educ + 0.0968 * Exper $$
异方差检验
残差的图形检验
最直观的方法是作模型残差平方 \(e_{i}^2\) 关于每一个变量的散点图,可能只有某一个变量与 \(e_{i}^2\) 的散点图表现出异方差特征。比较便捷的方法是用 \(e_{i}^2\) 对 \(Y_{i}\) 的估计值 \(\hat{Y_{i}}\) 作散点图。
resid = residuals(model)
plot(
resid^2 ~ fitted(model),
xlab = expression(widehat(Wage)),
ylab = expression(resid^2)
)
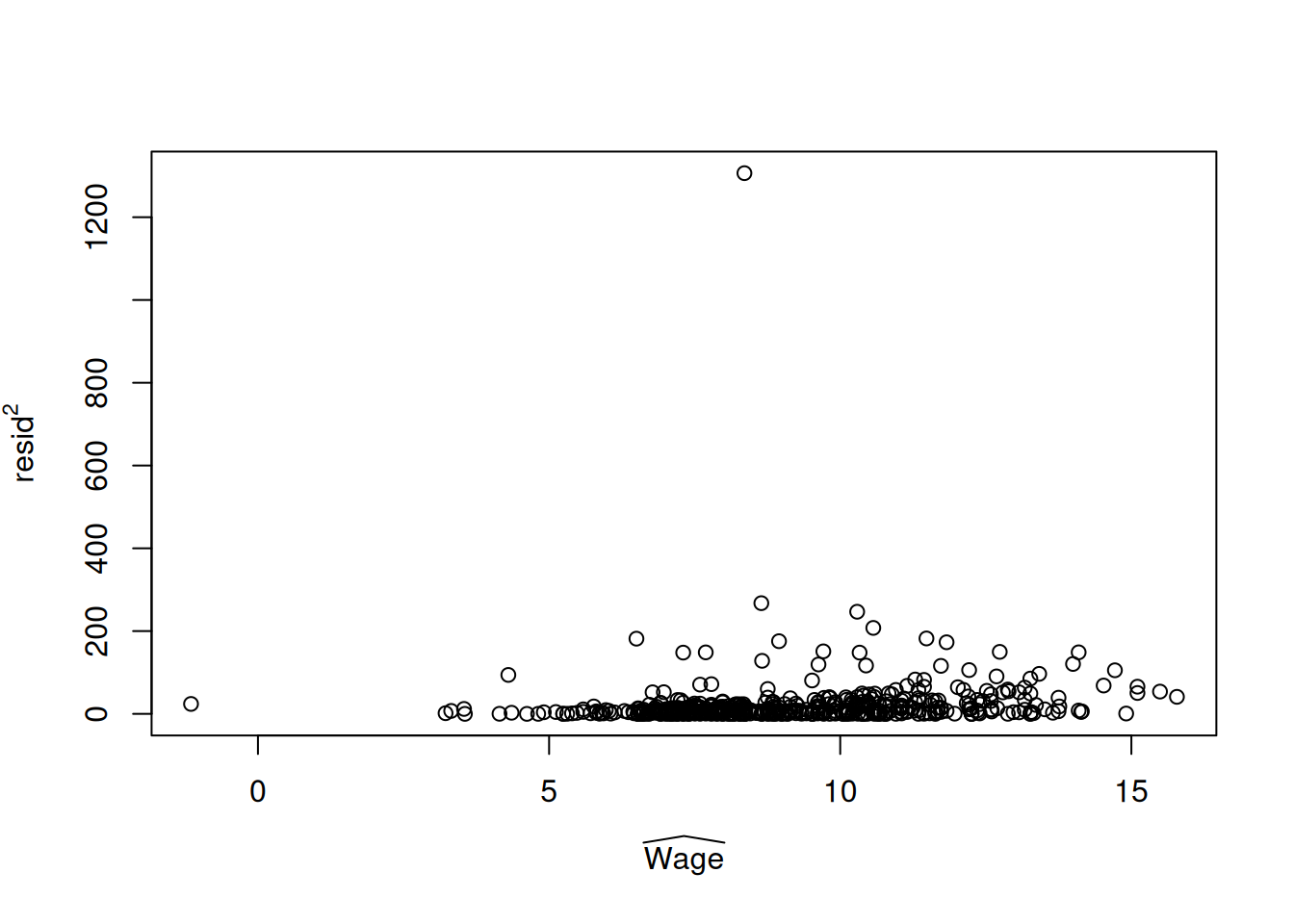
从图上可以看出残差平方与 \(\widehat{Wage}\) 之间存在某种线性关系,这些点并不是随机分布的,表明模型可能存在异方差。
White 异方差检验
# 建立辅助回归模型
model_aux = lm(
I(resid^2) ~ Educ + Exper + I(Educ^2) + I(Exper^2) + I(Educ * Exper),
data = data
)
summary(model_aux)
#>
#> Call:
#> lm(formula = I(resid^2) ~ Educ + Exper + I(Educ^2) + I(Exper^2) +
#> I(Educ * Exper), data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -42.3 -17.3 -10.4 1.1 1276.7
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 14.3830 71.3473 0.20 0.84
#> Educ -1.1833 9.1380 -0.13 0.90
#> Exper -1.4011 1.9121 -0.73 0.46
#> I(Educ^2) 0.1686 0.3007 0.56 0.58
#> I(Exper^2) 0.0271 0.0210 1.29 0.20
#> I(Educ * Exper) 0.0222 0.1041 0.21 0.83
#>
#> Residual standard error: 65.1 on 517 degrees of freedom
#> Multiple R-squared: 0.0215, Adjusted R-squared: 0.012
#> F-statistic: 2.27 on 5 and 517 DF, p-value: 0.0465
# 直接调用 lmtest 包进行检验
library(lmtest)
bptest(
model,
~ Educ + Exper + I(Educ^2) + I(Exper^2) + I(Educ * Exper),
data = data
)
#>
#> studentized Breusch-Pagan test
#>
#> data: model
#> BP = 11, df = 5, p-value = 0.05
在 5% 的置信水平下,辅助模型的 F 统计量的 p 值小于 0.05,说明整个模型显著,拒绝同方差原假设,White 异方差检验结果表明原模型存在异方差。
Breusch-Pagan 检验
bptest(model)
#>
#> studentized Breusch-Pagan test
#>
#> data: model
#> BP = 8.7, df = 2, p-value = 0.01
检验统计量的 p 值依然小于 0.05,Breusch-Pagan 检验结果也表明原模型存在异方差。
方差齐性检验
n = nrow(data)
m = ceiling(n / 2)
o = order(data$Wage) # order把顺序号计算出来
resid1 = model$residuals[o[1:m]]
resid2 = model$residuals[o[-1:-m]]
var.test(resid1,resid2)
#>
#> F test to compare two variances
#>
#> data: resid1 and resid2
#> F = 0.26, num df = 261, denom df = 260, p-value <2e-16
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#> 0.2059 0.3350
#> sample estimates:
#> ratio of variances
#> 0.2626
方差齐性检验结果表明,前后两个部分方差比值等于 1 的概率非常小,因此拒绝方差比值为 1 的原假设,即原模型存在异方差。
异方差的修正(注意 R 的 weights 参数设置)
利用原模型计算 1 / |残差| 作为权重来修正
w = abs(model$residuals)
model_w = lm(
I(Wage / w) ~ 0 + I(1 / w) + I(Educ / w) + I(Exper / w),
data = data
)
summary(model_w)
#>
#> Call:
#> lm(formula = I(Wage/w) ~ 0 + I(1/w) + I(Educ/w) + I(Exper/w),
#> data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.26 -0.99 -0.95 1.01 1.34
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> I(1/w) -4.44207 0.09530 -46.6 <2e-16 ***
#> I(Educ/w) 0.90621 0.00664 136.6 <2e-16 ***
#> I(Exper/w) 0.09505 0.00177 53.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.998 on 520 degrees of freedom
#> Multiple R-squared: 0.999, Adjusted R-squared: 0.999
#> F-statistic: 1.74e+05 on 3 and 520 DF, p-value: <2e-16
# model_w 模型的等价形式
model_glm = glm(
Wage ~ Educ + Exper,
weights = 1 / w ^ 2,
data = data
)
summary(model_glm)
#>
#> Call:
#> glm(formula = Wage ~ Educ + Exper, data = data, weights = 1/w^2)
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -4.44207 0.09530 -46.6 <2e-16 ***
#> Educ 0.90621 0.00664 136.6 <2e-16 ***
#> Exper 0.09505 0.00177 53.7 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for gaussian family taken to be 0.9966)
#>
#> Null deviance: 19100.41 on 522 degrees of freedom
#> Residual deviance: 518.23 on 520 degrees of freedom
#> AIC: 2283
#>
#> Number of Fisher Scoring iterations: 2
$$ \widehat{Wage} = -4.4421 + 0.9062 * Educ + 0.0951 * Exper $$
误差方法与 \(x_{i}\) 成比例:平方根变换
w = sqrt(data$Educ) # 这里以 Educ 变量为例
model_x_sqrt = lm(
I(Wage / w) ~ 0 + I(1 / w) + I(Educ / w) + I(Exper / w),
data = data
)
summary(model_x_sqrt)
#>
#> Call:
#> lm(formula = I(Wage/w) ~ 0 + I(1/w) + I(Educ/w) + I(Exper/w),
#> data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.262 -0.858 -0.183 0.567 9.653
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> I(1/w) -2.6456 1.0769 -2.46 0.014 *
#> I(Educ/w) 0.7814 0.0718 10.89 < 2e-16 ***
#> I(Exper/w) 0.0877 0.0164 5.36 1.3e-07 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.26 on 520 degrees of freedom
#> Multiple R-squared: 0.804, Adjusted R-squared: 0.802
#> F-statistic: 709 on 3 and 520 DF, p-value: <2e-16
$$ \widehat{Wage} = -2.6456 + 0.7814 * Educ + 0.0877 * Exper $$
误差方法与 \(x_{i}^2\) 成比例
w = data$Educ # 这里以 Educ 变量为例
model_x = lm(
I(Wage / w) ~ 0 + I(1 / w) + I(Educ / w) + I(Exper / w),
data = data
)
summary(model_x)
#>
#> Call:
#> lm(formula = I(Wage/w) ~ 0 + I(1/w) + I(Educ/w) + I(Exper/w),
#> data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.651 -0.250 -0.056 0.167 2.582
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> I(1/w) 0.0903 0.7622 0.12 0.91
#> I(Educ/w) 0.5854 0.0513 11.42 < 2e-16 ***
#> I(Exper/w) 0.0709 0.0138 5.13 4.2e-07 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.354 on 520 degrees of freedom
#> Multiple R-squared: 0.804, Adjusted R-squared: 0.803
#> F-statistic: 710 on 3 and 520 DF, p-value: <2e-16
$$ \widehat{Wage} = 0.0903 + 0.5854 * Educ + 0.0709 * Exper $$
其实本例中模型解释变量有多个,在这种情形下,可以 \(\hat{Y_{i}}\) 作为变换变量,而不是某一个解释变量,因为 \(\hat{Y_{i}}\) 是 \(X_{i}\) 的线性组合。
重新设定模型
通过对数变换压缩了变量的度量规模,因而有利于消除异方差。
model2 = lm(log(Wage) ~ log(Educ) + log(Exper), data = data)
summary(model2)
#>
#> Call:
#> lm(formula = log(Wage) ~ log(Educ) + log(Exper), data = data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.1125 -0.3321 0.0195 0.3192 2.0636
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.7946 0.2592 -3.07 0.0023 **
#> log(Educ) 0.9573 0.0917 10.44 < 2e-16 ***
#> log(Exper) 0.1662 0.0247 6.73 4.5e-11 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.47 on 520 degrees of freedom
#> Multiple R-squared: 0.194, Adjusted R-squared: 0.191
#> F-statistic: 62.5 on 2 and 520 DF, p-value: <2e-16
$$ \widehat{lnWage} = -0.7946 + 0.9573 * lnEduc + 0.1662 * lnExper $$
对数变换后仍然要进行异方差检验,检验步骤同上,此处不再赘述。
